Nous allons maintenant nous placer dans la 5D… Notre espace est donc défini en chaque point par R(O,x,y,z,t) où O est notre observateur de référence. Comme par définition O ne bouge pas par rapport à l’espace qu’il observe, nous devons considérer que son horloge fait référence où qu’il soit. En 5D nous avons donc un centre objectif pour tout l’espace = l’observateur. Puisque tout objet qui n’est pas immobile par rapport à lui dans l’espace N’EST PAS dans le même espace d’observation, il est soit à t+delta t, soit à t-delta t, mais pour de petites vitesses devant C, delta t est faible et donc cette distance temporelle ne prend pas tout son sens.
En effet la Relativité nous pousse à décrire que R’ (O’,x’,y’,z’,t’) est tel que les distances spatiales et temporelles sont pour O’ déduites de celles mesurées dans R en les multipliant par : Gamma = 1/racine(1-V²/C²), V étant la vitesse de R’ relativement à R. Nous allons prendre ce résultat comme base.
Notre travail va consister maintenant à tenter de comprendre ce qui se passe dans R et dans R’ quant aux observations des « mêmes objets ». Nous supposerons que V est très proche de C, aussi proche que l’on veut, parce que notre objectif final sera de « sauter le pas » pour nous plonger dans C totalement…
Nous n’avons même pas à imaginer que O’ accélère, il n’accélère pas, simplement nous considérerons des R’ sucessifs à des vitesses de plus en plus proches de C. D’ailleurs l’accélération, même d’un objet continu qui perd de l’énergie régulièrement, a une limite par rapport à un référentiel initial, puisqu’on est borné par C en vitesse. L’accélération ne saurait donc être constante, simplement, forcément, pour tout objet, elle passe par un maximum quel que soit l’objet continu considéré, par rapport au référentiel initial.
Soit dans R l’ensemble des objets de vitesse faible par rapport à O. Alors dans O’ ces objets sont transformés, écrasés selon la direction de V par Gamma, MAIS PAS SEULEMENT ! En effet l’horloge fait aussi que le t’ de l’objet considéré est très petit ! Pour O’ quand disons une étoile fait 1 milliard de tours sur elle même dans O, cela dure … 0,001 seconde ou encore moins pour O’ (aussi peu que l’on veut puisqu’on est aussi proche de C que l’on veut selon R’).
Ecrasé dans une direction de la taille d’une particule aussi petite que l’on veut… Et étalé dans la direction perpendiculaire à la direction de V de la taille d’une étoile et plus ! (la lumière émise par l’étoile, doit faire aussi considérer qu’un « champ » semble émaner de cette particule pour O’). Mais en sus « l’étoile » (c’est une étoile pour R) TOURNE très très vite… Et même CHANGE de place très très vite (pensez en 1 milliard de tours sur elle même combien de tours galactiques l’étoile fait ?), à tel point qu’il est impossible de savoir où et quand on peut la trouver à part « à peu près » pas trop loin de l’endroit où on l’a perçue un peu plus tôt… à l’échelle de la Galaxie pour R, à l’échelle du rayon galactique selon R’, d’un facteur cos(teta)/racine (1-V²/C²) où teta est l’angle que fait V avec le plan galactique…
Plus je prends un référentiel R’ proche de C et plus ces notions de 1) rotation de l’étoile , 2) déplacement dans le plan galactique, et 3) écrasement de la distance selon la direction de V, font que mon étoile « perd une dimension » (écrasement d’une distance), et s’étale dans les 3 autres, la faisant ressembler à un truc qui se balade très très vite dans un petit un morceau de plan (le plan galactique), qui lui même étant « tournoyant » s’inscrit dans un petit volume…
Petit, rapide, imprévisible, centré mais étalé aléatoirement dans l’Espace, ça ne vous fait penser à rien ? Moi si.
A noter que sur de longues périodes de temps (dans R) on ne sait pas prédire ne serait-ce que le mouvement relatif de trois corps en « interaction gravitationnelle », pour cause de « cahos »… Dans R’ cette indétermination prend des proportions considérables, quoiqu’il reste une présence relativement centrée autour du point de mesure initial (l’inertie dans R, se retrouve dans le centre aléatoire dans R’).
INVERSEMENT.
Ce qui paraît « Petit, rapide, imprévisible, centré mais, étalé aléatoirement dans l’Espace » pour R’ est en fait une Etoile se baladant tranquillement à un rythme de tortue dans sa Galaxie pour R.
R et R’ étant équivalent, le voyage est bouclé… R et R’ ne peuvent presque pas communiquer entre eux parce qu’il y a un brouillage de type « fractal », les mêmes choses sont là, exactement, mais n’ont pas du tout les mêmes propriétés ni spatiales, ni temporelles, ni donc même causales, ce qui est une seule chose dans R, semble être réparti un peu partout pour R’ et inversement.
Et pour C ? Eh bien pour C c’est simplement Lim « max » de R’, et le brouillage est total. En effet tout volume dans R aussi grand que l’on veut, constitué des objets de vitesse < C, se voit réduit de plus en plus quand on se place dans un R’ proche de C, toute l’histoire de R se trouve accélérée, toute la causalité de R est perçue de façon cahotique et indiscernable dans R’, tous les objets semblant s’éloigner de plus en plus vers O le centre de R, point de fuite de V, nous avons là la constitution d’un trou noir. Ce trou noir constitué dans un R’ ayant la vitesse V =quasi C /R , simplement un « saut » en fait très continu, dans un R’ proche, constitue dans un repère un saut discontinu parce que spatio temporellement brouillé pour les mêmes raisons, de l’émission d’un photon, ou dans l’autre l’effondrement final d’un trou noir. Ces deux repères choisis coupent définitivement tout lien causal direct existant entre les deux repères R et R’, quoique représentant exactement le même Univers…
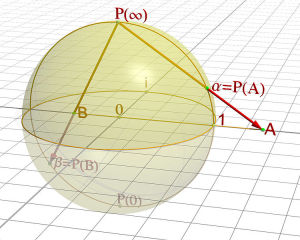
Ces deux repères R(O,x,y,z,t) et R'(O’,x’,y’,z’) se trouvent donc EXACTEMENT semblables d’un point de vue topologique / mathématique à une boule de Rieman posée sur une sphère, pour deux espace temps 4D, l’un plat, l’autre sphérique (relativement au premier) dans un espace 5D. Ces deux espaces sont EXACTEMENT LES MEMES, mais on passe de l’un à l’autre par une TRANSFORMATION DE TYPE RIEMANN.
Et pour être plus précis dans l’image comme je l’ai précisé en tout début de post, ce qui est perçu étant compris entre t-delta t et t+delta t :
Tout ce qui est dans le plan R’ file à C – en fuite par rapport à O – tandis que dans le plan R’, R est un trou noir. Inversement, il existe un repère R » filant à C dans R’ relativement à O’ quelconque dans R’ (c’est bien un type de changement de repère sphérique centré et pas « uniforme » dans une direction donnée !) pour lequel R’ est un trou noir. Pour autant dans R » la transformation de R inclu dans R’ n’implique pas du tout que R soit un trou noir dans R ». C’est la transformation des objets de tout R, qui se retrouve spatialement étalée dans l’espace R ».
C’est pourquoi on ne doit pas parler de 5 dimensions mais de 10 directions. Ce n’est pas la même chose selon la vitesse relative dans R que de passer dans un R’ à V ou -V, quant à la transformation de l’objet considéré. La direction de V prend un sens primordial. On ne peut plus raisonner sans la direction du vecteur.
Il faut alors considérer chaque objet physique comme étant réellement 1) Etalé dans tout l’espace, 2) Centré aléatoirement et 3) Constitué d’une énergie massique ou pas
Espace, Centre, Energie, sont donc les trois seules dimensions qui nous permettent de transformer tout objet spatialement étalé au sein d’un espace de référence R, en le composant unique ou mélangé à d’autres objets dans R’, par une transformation de type Sphère de Riemann…
La suite bientôt ami lecteur (je sais tu n’es pas nombreux, et alors ?! 🙂 )

Balèse !