Une autre métrique de l’espace-temps est possible, qui en change le paradigme fondamental. Elle est fondée sur la réflexion que, la vitesse de la lumière étant donnée, invariante selon l’observateur, la définition du temps fondée sur un élément local tel que celle fondée sur l’atome de Césium ne convient pas.
En effet il n’y a pas toujours eu d’atome de Césium, et il n’y en aura pas toujours non-plus dans l’histoire de l’Univers.
Qui plus est, on constate qu’il faut tenir compte du champ gravitationnel et de la vitesse, pour adapter le temps mesuré en R1, en référence à tel ou tel référentiel R2.
Or ceci est la poule et l’oeuf ! Car vitesse et champ gravitationnel ne peuvent se définir sans que le temps soit préalablement connu ! Donc pour mesurer le temps, je dois d’abord connaître le temps, qui me permet d’établir vitesse et gravitation me permettant de… mesurer le temps…
Maintenant on peut se demander : mais est-il possible de définir le temps autrement, étant donnée la seule base qui serait la vitesse de la lumière ? Oui ! C’est possible ! Et c’est possible en référence à un changement axiomatique concernant la définition de notre métrique spatio-temporelle.
Nous acceptons le fait que l’Univers est en expansion, mais ce qui est un point de vue là aussi parfaitement relatif. C’est équivalent à dire que l’Univers est stable mais que ce sont les objets physiques et les vitesses qui sont en contraction, comme nous l’avons montré lors de notre précédent post.
Or que ce passe-t-il dans un tel Univers ? La Fréquence, ou la Longueur d’onde de la lumière se décalent « vers le rouge », que ce soit dans l’espace, en fonction de la distance relative de deux objets, ou dans le temps si l’on considère un « même objet physique » entre deux dates (car il s’éloigne), relativement à l’observateur.
Nous définissons alors comme unité de distance d (et donc aussi de temps = d/c) : la distance à partir de laquelle le décalage spectral de la lumière est divisé par deux (ou par 10, ou par n’importe quelle fraction) dans l’Univers Observable. Cette définition ne dépend pas du temps, car tant que de la lumière est observable on peut toujours établir la mesure de cette unité.
On notera ici que cette possibilité de définition est permise par une autre propriété fondamentale de la lumière : sa dualité onde / corpuscule. C’est donc en comparant directement les distance des longueurs d’ondes mesurées que l’on pourra établir notre unité.
De plus pour tout temps, un élément quelconque (Cesium, mais tout aussi bien autre chose si dans l’Univers il n’y a pas un tel atome présent au temps ou à la place de d’observation considéré), placé en deux endroits distants, on peut noter mathématiquement le décalage spectral obtenu, qui nous donnera donc une mesure de notre unité qui ne dépend pas d’éléments particuliers se trouvant là ou pas dans l’histoire de notre Univers.
La conséquence première de cette définition est donc une définition du temps ne dépendant que de la lumière et de l’espace(t) relativement à l’observateur. Ceci éliminant donc toute référence à un « élément atomique » épiphénomène non-indépendant de l’observateur quel que soit sa nature ou l’époque considérée.
La conséquence seconde est que cette axiomatique impose de revoir la métrique de l’Univers sur cette base, et donc y compris les opérateurs de transformation entre observateurs. Il n’est pas donné que deux observateurs puissent s’accorder, hors l’accord sur cette base de définition, sur un « même espace-temps », autrement dit sur la présence dans ce « même espace-temps » des mêmes « objets physiques », selon leurs vitesses relatives (ou champs de gravitation locaux). Mais ils partagent pourtant une définition invariante entre eux, de la lumière, de la distance et du temps, qui ne dépend que de la compréhension de l’expansion / contraction de l’Univers.
De la même façon, la définition historique du mètre s’est fondée sur la seule compréhension de la courbure de la surface de la terre. Parce que l’on a intégré le fait que la courbure de la terre définissait une sphère on a pu définir son diamètre comme unité de distance.
Parce que l’on a intégré le fait que l’Univers est en expansion/contraction, on peut définir le temps sur le seul décalage spectral de cette même lumière dans l’espace.
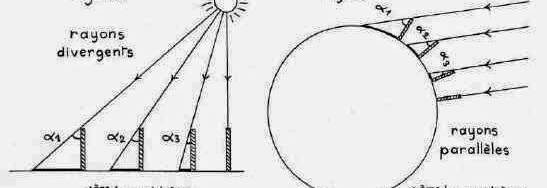
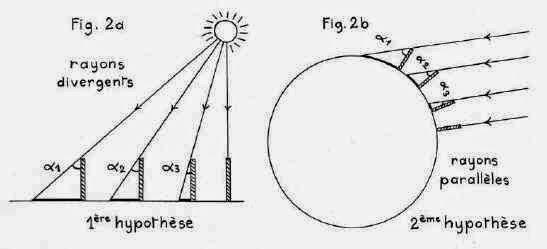
Comment ces deux approches sont-elles comparables ? L’acceptation de la courbure de la terre, permet d’en calculer la valeur, il faut et il suffit d’observer, comment les angles ou hauteurs apparents changent avec la distance.
Si on n’accepte pas la courbure, on interprétera la mesure comme due à « la distance du soleil », si on accepte la courbure et la très grande distance du soleil, et donc le parallélisme local de ses rayons, on en déduira le rayon de la terre sphérique.
De la même façon concernant l’univers, si on accepte l’expansion / contraction, et l’invariance de la vitesse de la lumière, alors on en déduit des unités de distance et de temps qui ne dépendent pas d’un autre élément.
Mais alors on ne peut plus du tout considérer l’Univers de la même façon. La métrique ayant changé en une métrique expérimentale plus simple, plus fondamentale, la façon même de concevoir la relation Univers / Observateur n’est plus du tout la même.
Il faut tout revoir.