Il est fondamental et très important de se pencher sur le problème Relativiste pour avancer non seulement sur la 5D, mais aussi sur la nature de l’esprit. Nous attaquerons sur ce post le problème des sphères de temps associées à un disque de matière. Pour cela nous nous pencherons sur la notion de rayon de Schwarzschild, et son application directe à la mesure d’un temps dt1 compté à partir du centre du disque de matière (distance r), par rapport au temps dt2 d’un observateur très lointain de ce disque. Il s’agit du problème de la dilatation du temps !
Etant donné le disque de matière de masse et rayon (M0,r0) on a :
Avec Rs0 = 2GM0 / c² = « Rayon de Schwarzchild du dique de matière ».
En faisant l’hypothèse simple que le disque de matière est homogène, et donc que la quantité de matière à une distance r du centre est M(r) = M0.r²/r0², ce qui permet de retrouver le résultat pour r < r0, et pour r > r0 la quantité de matière à prendre en compte ne bouge plus M(r) = M0.
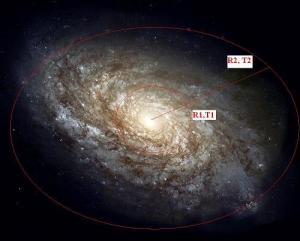
Petit dessin galactique :
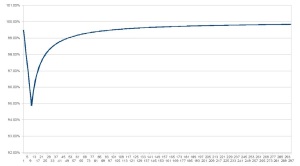
Et donc la fonction considérée prend cette forme pour dt1, pour une disque de matière égal à 10 fois son rayon de Schwarzschild :
Le pincement de la courbe correspond au bord du disque de matière…Où dans ce cas précis dt1 = 95% dt2, c’est à dire que le temps s’écoule le plus lentement au BORD DU DISQUE par rapport à l’observateur lointain, qui se trouve avoir la même horloge que l’observateur central (dt1 = dt2 au centre comme à l’infini…).
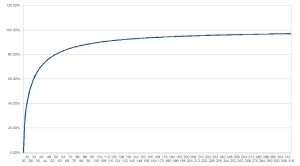
Dans le cas d’un trou noir on a la courbe qu’à partir du pincement, vers la droite… Comme ceci : (r0 = rayon de Schwarzschild) :
Cela signifie que l’évolution normale d’un disque de matière suffisamment massif, propose des sphères temporelles dont les temps relatifs sont semblables à la première courbe, pour aller vers la deuxième… Il faut alors se faire le film de ce à quoi ça peut ressembler pour l’observateur lointain qui regarde ça…
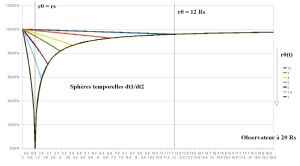
Voici la suite des courbes retraçant les sphères temporelles lors de l’histoire de l’effondrement du disque, par rapport à un observateur se tenant à 20 rayons de Schwarzchild d’un disque initial d’un rayon de 12 Rs…. Au delà de r0 les courbes se rejoignent toutes, ce qui est normal…
Le temps étant relatif, je ne vois donc aucune différence entre l’intérieur d’un trou noir et l’expansion de l’Univers depuis le Big Bang… Il semblerait qu’il n’y ait de différence que de nature temporelle entre le dedans et de le dehors, où la causalité est différente dedans que dehors, elle n’est pas inversée, mais elle est différente. Je l’affirme parce que pour O2 il y a bien une différence notable entre l’évolution causale des phénomènes jusqu’au bord du disque, puis son évolution jusqu’au centre, mesurée grâce à son horloge qu’il suppose universelle, et qui le lie en fait à un point de vue causal relatif.
La pince temporelle de bord du disque n’est pas différente qu’il soit un trou noir ou pas, c’est simplement le choix de l’observateur O2 de considérer une causalité égale entre le dedans et le dehors, qui le pousse à adopter la même horloge (définition d’une causalité égale), et qui donc ne sait pas décider de ce qui se passe sur la pince où ce temps relatif s’annule, tout simplement parce que son horloge (Césium par exemple) n’existe plus, et n’est plus à même de donner un signal, parce que le Césium ne peut aller à C, étant massif… alors que cette frontière est instable, toute particule qui s’y situe bascule d’un côté ou de l’autre, dans le trou noir ou à l’extérieur en fonction d’une vitesse directionnelle donnée, et qui est soit faible soit proche de C.