Auteur/autrice : galuel

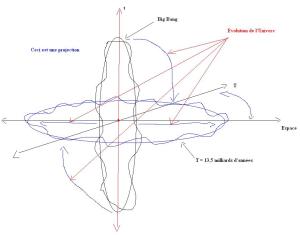
Voici une projection d’un Univers 5D pris à deux temps T = 0 et T = 13 milliard d’années.

Prenons la Relativité, qu’est-ce qu’elle suppose ? Par hypothèse que la lumière a une vitesse maximale et constante C, et en déduit que la lumière se déplace en « ligne droite », et que donc si elle dévie c’est en fait l’espace temps qui est courbe…

Bon maintenant on pourrait approcher ce résultat d’une autre façon.

On peut supposer – et c’est une hypothèse raisonnable – que l’espace est parfaitement sphérique, que la lumière suit toujours un équateur, et que l’espace local n’est pas courbé par la matière, mais qu’il s’agit uniquement de courbure de type temporelle.

En effet, si je me place en position comobile, si je mets deux horloges H1 à proximité du centre d’un système massif, et H2 loin de ce centre, alors je constate que H2 avance plus vite que H1, cette interprétation est valide de ce point de vue.

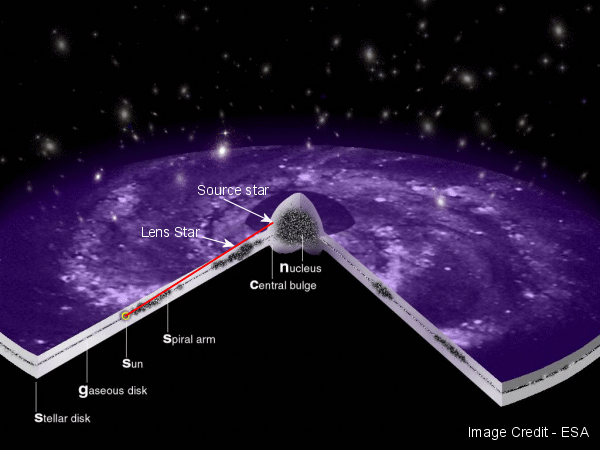
Je dois alors considérer que ce système massif local (par exemple une Galaxie), se comporte comme un espace 4D local complet, où des tranches sphériques 3D, se comportent comme un espace (3D+t) avec un temps universel – dans cette tranche -. Quand je considère deux atomes de Césium Cs1 dans une tranche sphérique (3D+t) T1 et Cs2 dans une tranche T2 plus éloignée, je constate que Cs2 a une durée de vie plus courte que Cs1.

Ce qui courbe alors la trajectoire de la lumière n’est pas une courbure de l’espace qui est sphérique, mais des puits temporels locaux.

Je peux alors considérer qu’il y a non pas un temps dans l’Univers mais des temps sphériques t locaux, qui ont des vitesses Vt différentes. De Vt = zéro à la surface des trous noirs, à VT = 1 par convention (Vitesse du temps comobile), essentiellement dans l’espace situé à bonne distance de tout puits temporel.

Tous ces temps locaux sont observables et mesurables, leur vitesse d’action est Vt < VT, le temps t sphérique local est de la forme t = T x Vt/VT, avec Vt qui tend vers zéro à l’approche d’un trou noir.

Je dois donc considérer l’Univers comme étant une sphère 3D en expansion dans un espace 5D, où il y a deux dimensions de temps, l’une universelle de temps T = âge de l’Univers, l’autre locale de temps t = (Vt / VT) T avec (t / T) < 1.

Ces deux dimensions sont des mesures libres outre cette relation, car t dépend du temps T0 de sa création (ex : création d’une galaxie, d’un trou noir) pour commencer, et de la masse totale locale pour sa vitesse 0 < Vt < 1 (qui peut donc aussi varier selon l’origine choisie, et l’ajout ou pas de masse selon T à considérer).

On peut alors se visualiser l’Univers comme suit :

Un cercle de dimension spatiale posé à plat, vibrant localement comme la corde d’une guitare, qui grossit à chaque seconde et commence d’un tout petit cercle à T = zéro (le big bang). Les vibrations locales sont des puits temporels locaux que sont les galaxies, les Etoiles très massives, ou les trous noirs.

L’évolution de la densité de rayonnement et donc de la pression exercée par ce rayonnement sur un Volume V(t) depuis le Big Bang est quelque chose qui se mesure en 1/R(t)^4, où R est le rayon de l’hypersphère Univers dans laquelle baigne V(t).

Pour vous faire une image en 3D, considérez une sphère en 2 dimensions, un volume serait alors représenté par un mini disque sur cette sphère. Ce minidisque recevrait alors une pression inversement proportionnelle puissance 4, au rayon de la sphère 2D sur lequel il est placé. L’univers en expansion, c’est la sphère 2D qui part de zéro (le big bang), et qui grossit dans le temps. Plus la sphère grossit moins la pression est forte, mais plus le disque est en fait petit par rapport à la surface totale de la sphère 2D.

Maintenant considérons la chose suivante… Imaginons un Volume V(t), et considérons que ce Volume est sous pression en 1/R(t)^4 donc avec R(t) = Volume de la sphère d’espace de dimension supérieure dans lequel baigne V(t).

Et que cette force diminue V(t)… Ce qui semble logique…

Etant donné que l’expansion de l’Univers est équivalent à constater que les objets diminuent de volume les uns par rapport aux autres, et que l’on fait l’hypothèse que tout est dû à cette force, et à rien d’autre.

Quelle serait l’expression de la diminution de V(t) en chaque point de l’Univers en fonction de cette force en 1/R(t)^4 étant donné l’expansion constatée de l’Univers ?